波数与波长的关系

波数与波长的关系如下：

波数等于真实频率除以光速，即波长（λ）的倒数，理论物理中定义为：。意为2π长度上出现的全波数目，从相位的角度出发，可理解为：相位随距离的变化率（rad/m）。

波数与波长是描述光的性质的两个重要参数，它们之间的关系可以通过普朗克-爱因斯坦公式以及光速公式来解释。

波数的定义和计算方法详细介绍：

波数是指单位长度或单位距离内所包含的波峰数或波谷数，通常用 cm^-1 作为单位。波数的计算方法为：

波数 = 光速 / 波长

其中，光速为 299792458 m/s，波长为光的波长，单位为 m。

波长的定义和计算方法

波长是指一条波形中两个相邻的峰或谷之间的距离，通常用 nm、μm 或 m 等作为单位。波长的计算方法为：

波长 = 光速 / 波数

其中，光速和波数的单位与上述相同。

波数与波长的关系

波数与波长之间有一个反比例关系，即波数越大，波长越小。这个关系可以通过普朗克-爱因斯坦公式以及光速公式来解释。

普朗克-爱因斯坦公式描述了光子能量与频率之间的关系：

E = hν

其中，E 为光子的能量，h 为普朗克常数，ν 为光子的频率。

将公式改写为：

E = hc / λ

其中，c 为光速，λ 为光的波长。将能量代入公式中可得：

hc / λ = hν

化简后得：

λν = c

即波长和频率的乘积等于光速。根据波数和波长的定义和计算方法，可以将上式改写为：

ν = c / λ = 光速 / 波长 = 波数 × 光速

因此，波数和波长之间的关系为：

波数 = 光速 / 波长

或

波长 = 光速 / 波数

波数和波长是描述光的性质的两个重要参数。波数定义为单位长度或单位距离内所包含的波峰数或波谷数，用 cm^-1 作为单位；波长定义为一条波形中两个相邻的峰或谷之间的距离，用 nm、μm 或 m 等作为单位。波数和波长之间存在反比例关系，可以用普朗克-爱因斯坦公式和光速公式来解释。

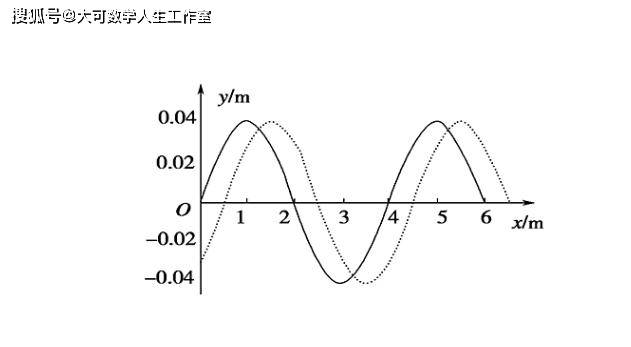
波长对波性质的度量

波长（或可换算成频率）是波的一个重要特征指标，是波的性质的量度。例如：声波可以从它的频率来量度，人耳可听的声波从20Hz到20kHz，相应的波长从17m到17mm不等；人眼的可见光从深红色的760nm波长，到紫色的390nm波长。

在讨论弹性波的传播时，会假设媒质是连续的，因为当波长远大于媒质分子之间的距离时，媒质中一波长的距离内，有无数个分子在陆续振动，宏观上看来，媒质就像是连续的; 但如果波源的频率极高，波长极小。

当波长小到等于或小于分子间距离的数量级时，相距约为一波长的两个分子之间，不再存在其他分子，不能再认为媒质是连续的，也不能传播弹性波了。高度真空中分子间的距离极大，不能传播声波就是这个原因。

横波与纵波的波长

波长指沿着波的传播方向，在波的图形中两个相对平衡位置之间的位移。横波与纵波的波长所代表的意义是不同的。在横波中，波长是指相邻两个相位相差

的点的距离，通常是相邻的波锋、波谷或对应的过零点。在纵波中，波长是指相邻两个密部或疏部之间的距离。波长在物理中常表示为λ，国际单位是米（m）。

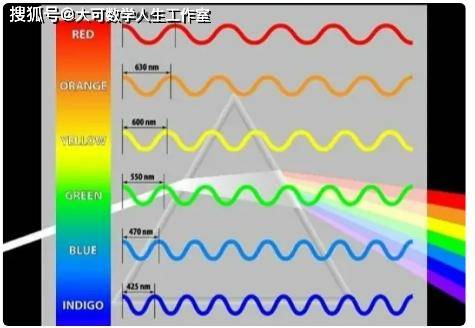
原子、分子和原子核的光谱学中的频率单位。符号为σ或v。等于真实频率除以光速，即波长(λ)的倒数，或在光的传播方向上每单位长度内的光波数。在波传播的方向上单位长度内的波周数目称为波数（常写为k），其倒数称为波长，k=1/λ。

理论物理中定义为：k=2π/λ。意为2π长度上出现的全波数目。从相位的角度出发，可理解为：相位随距离的变化率（rad/m）。与波数对应的矢量称为波矢量。

来自：文燕爱教育